5.1 The RGB Colorspace

The RGB colorspace is important to us because it is what we see when we look at a color monitor. The monitor mixes together different amounts of red, green, and blue primaries. Because of this, the colors that can be seen on a computer monitor can be represented as triples of numbers or as vectors in a three-dimensional cube.  The amount of each primary contained in a color can be represented by a number in a fixed range. Because the GIMP uses 8 bits per primary color channel, the range per primary is 0 to 255 (2⁸=256). Here, 0 means no primary is used and 255 means that there is as much primary as the monitor can produce. Although there are issues with white balance, calibration, and human visual perception, it is presumed that the three primaries combined at full strength produce white and the three combined at zero strength produce black. Of course, the black produced is no deeper than that of the monitor when turned off.

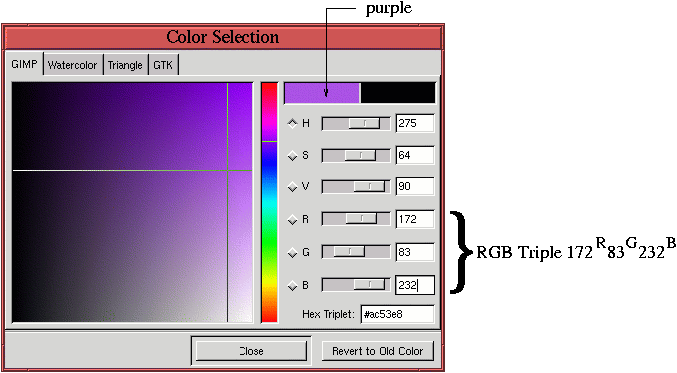
When it is useful to talk about colors in numeric terms, as it is in Chapter 6, which discusses color correction, we will use a special notation to designate colors. For example, the purple composed of a red at 172, a green at 83, and a blue at 232 will be denoted 172^R 83^G 232^B. This color is illustrated in Figure 5.1,

  

Figure 5.1: Representing a Color with an RGB Triple: Purple= 172^R 83^G 232^B

which shows how the color is composed using the Color Selection tool. This tool is opened by clicking on the Active Foreground Color or Active Background Color patches in the toolbox. The tool dialog can be used to display RGB colors. These are dialed in using the sliders or can be entered numerically. The selected color appears in a patch at the upper right of the dialog. What we have here is digital finger paint!

As you will see later in this chapter, it is useful to think of the triples formed by the primaries as a color cube where each of the primaries forms one of the principle axes. The RGB color cube is illustrated in Figure 5.2.

  

Figure 5.2: The RGB Color Cube

Each axis of the cube represents values of red, green, or blue in the range [0,255]. The red axis, labeled R, shows the associated color scale beneath it. The green and blue axes are illustrated similarly. As mentioned earlier, 0 means that the monitor does not emit the primary color and 255 means that it emits the maximum. Values between 0 and 255 yield gradations in the color's intensity.

As the word colorspace implies, colors act like vectors. They can be combined by addition and subtraction to obtain other colors in the cube. Thus, the origin of the cube, or 0^R 0^G 0^B, represents the total absence of color, which is black. The far corner from the origin is the sum of the highest intensities of red, green, and blue, or 255^R 255^G 255^B. This produces the color white, which is why this corner of the cube is labeled W in Figure 5.2. The other corners of the cube represent the various primary and secondary colors. We've already encountered red, green, and blue. The remaining three are cyan, magenta, and yellow. From the labels in Figure 5.2, it can be seen that adding 255 red to 255 green makes 255^R 255^G 0^B or yellow, adding 255 red to 255 blue makes 255^R 0^G 255^B or magenta, and adding 255 green to 255 blue makes 0^R 255^G 255^B or cyan.

Note that the main diagonal of the RGB cube is illustrated in Figure 5.2 as a line drawn between the black origin at 0 and white at W. This line represents the colors in the RGB cube that consist of equal amounts of red, green, and blue. All the points on this line are gray. The closer to the origin, the darker the gray; the closer to W, the lighter. It is for this reason that the main diagonal of the RGB cube is referred to as the neutral axis  . Grays are neutral because they prefer no hue; they contain equal quantities of red, green, and blue.

©2000 Gimp-Savvy.com